머신러닝(Machine Learning) 12장
- XOR 문제 딥러닝으로 풀기(Backpropagation) -
앞장에서 딥러닝의 기본 개념에 대해서 살펴보았는데 XOR 문제가 발생하였다. 비교 연산을 하는 경우 AND의 문제나 OR의 문제는 하나의 logistic regression을 사용하게 되면 쉽게 해결 할 수 있었다. 하지만 XOR의 경우에는 하나의 logistic regression을 이용하면 해결하는 방법이 없었다. 이 때 사용한 방법이 logistic regression을 multiple로 사용하는 방법이다. 이는 Neural Network의 형태로 나타나게 된다. 이런 경우 풀 수 있는 가능성은 있지만 학습에 대한 불가능이 나타나게 되었다.
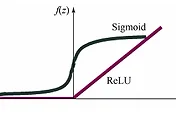
우선 XOR 문제를 Neural network를 이용하여 어떻게 해결을 할 수 있는지를 살펴보자. 학습을 시키는 방법이 아니라 우선적으로 W와 b에 대한 값을 임의로 만들어주어서 Multiple logistic regression의 상황에서는 해결을 할 수 있는지를 살펴보는 것이다. 예시를 살펴보면서 x1과 x2의 입력 값에 대한 결과 값이 제대로 나오는지를 살펴보자. 입력 값의 종류는 네 가지로 구분 될 수 있으므로 네 가지의 경우를 모두 사용하여 결과 값을 비교해보도록 하자. XW + b의 값을 구하게 되고 이를 sigmoid 함수에 넣어서 결과 값을 얻게 된다.
우선 (0, 0) 으로의 값을 먼저 넣게 되면 다음과 같은 결과가 나타나게 된다. 이는 y1과 y2라는 결과가 나오게 되고 이 값을 다시 또 다른 logistic regression 모델에 넣게 된다. 그래서 나타나는 결과 값을 판단하여 XOR의 답으로 해석하게 된다.
모든 값에 진행하게 되면 XOR에서 원하는 결과 값이 multiple logistic regression인 Neural Network를 통해서 예측을 할 수 있다는 것을 보여줄 수 있다.
이를 쉽게 다시 구성을 하여 만들게 되면 다음과 같은 형태의 구조로 나타나게 된다. 각각의 w와 b의 값을 가지게 되는 logistic regression이 3개 존재하는 Neural Network의 형태이다.
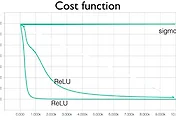
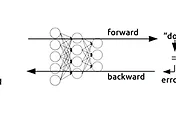
이로써 Neural Network를 이용하게 되면 XOR 문제를 해결할 수 있다는 것을 알게 되었다. 하지만 어떻게 하면 이러한 w와 b 값을 학습시킬 수 있는가에 대한 문제가 생기게 된다. 위의 경우처럼 임의로 값을 지정하는 것이 아니라 데이터를 입력하면 기계적으로 학습하여 w와 b를 학습할 수 있는 방법이 필요한 것이다. 하나의 logistic regression에 대한 학습을 시키는 경우에는 cost function을 gradient descent algorithm을 통해 최솟값을 가지도록 하는 방법으로 학습을 시켰다. gradient descent algorithm을 사용하기 위해서는 기울기를 구하기 위해 미분을 사용하는데 Neural Network으로 가게 되면 하나의 logistic regression이 아니므로 미분을 하는 것이 매우 복잡하게 되었다. 그래서 나온 방법이 바로 Backpropagation이다. 이는 forward를 통해 나온 결과 값과 실제 데이터를 비교하여 이에 대한 차이를 뒤로 가면서 학습을 시키는 방법이다.
Back propagation의 방법을 알아보도록 해보자. 다음과 같은 형태의 Neural Network가 있다고 생각해보자. 두 개의 logistic regression을 가지고 있다. g라는 모델은 w와 x의 곱을 계산하는 것이고 f의 경우에는 g의 결과 값과 b를 더하여 나오게 된다.
이 때 각각의 입력 값이 최종 결과 값에 미치는 영향을 알고 싶다. 이는 결과 값에 대한 각각의 입력 값의 편미분을 통해서 구할 수 있게 된다. 첫 번째 순서는 forward 방법으로 학습 데이터에서 특정 값을 입력 값으로 넣어주게 된다. 이를 통해 결과 값을 구할 수 있다. 다음으로 backward로 입력 값에 대한 편미분을 통해 영향을 끼치는 정도를 구하게 되어 학습을 진행할 수 있는 것이다. 편미분을 진행하는 것은 chain rule에 의해 각각의 layer를 넘어가면서 편미분의 값을 구해주게 되면 최종 입력 값에 대한 최종 결과 값의 편미분을 구할 수 있게 된다.
'머신러닝' 카테고리의 다른 글
| 머신러닝(Machine Learning) 14장 - 딥러닝 weight 초기화의 중요성 - (0) | 2017.06.01 |
|---|---|
| 머신러닝(Machine Learning) 13장 - ReLU function - (0) | 2017.06.01 |
| 머신러닝(Machine Learning) 11장 - 딥러닝(Deep Learning) 기본 개념 - (0) | 2017.05.29 |
| 머신러닝(Machine Learning) 10장 - Training-Testing data set - (0) | 2017.05.29 |
| 머신러닝(Machine Learning) 9장 - Learning rate, data preprocessing, overfitting - (1) | 2017.05.29 |