머신러닝(Machine Learning) 8장
- Softmax regression의 cost함수 -
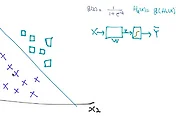
우리는 앞장에서 여래 개의 결과 값을 가질 수 있는 형태의 regression에 대해 살펴보았다. 각각의 데이터에 대해서 binary 형태의 선형 구분을 해주어 이에 따라 각각에 대한 알고리즘을 실행시켜 해당하는지 아닌지를 예측하게 되었다. 이를 위해 행렬의 형태를 사용하게 간단하게 표현을 할 수 있었다.
우리는 또한 결과 값이 sigmoid function을 통해 0과 1사이의 값을 가지게 만들고 싶었다. 그래서 각각의 알고리즘을 돌린 결과에 대해 p라는 확률적인 값을 가지게 만들고 싶다. 이런 방법을 해주는 것이 바로 Softmax라는 기법이다.
특정 데이터 결과 값들에 Softmax라는 함수를 넣어주게 되면 p라는 확률적인 값으로 결과 값을 바꾸어주게 된다. 그렇게 되면 각각의 데이터 결과 값은 0과 1사이의 값을 가지게 되고 또한 모든 결과 값을 더한 값이 1로 나타나게 된다. 우리는 위와 같은 확률적인 결과 값을 통해 높은 확률을 가지는 결과를 예측되는 결과 값으로 생각하게 된다.
데이터를 학습하기 위해서는 Cost function에 대한 정의가 필요하다. Cost function은 실제 데이터의 결과 값과 알고리즘을 통해 예측하는 값의 차이를 계산하는 것이다. Cost function을 최소화 시키는 알고리즘을 찾음으로써 궁극적으로 가장 적절한 예측을 할 수 있는 가설을 찾을 수 있는 것이다. 위와 같이 여러 개의 결과 값을 사용하게 되는 경우 어떻게 Cost function을 구할 수 있을까? 그 방법은 바로 Cross-entropy라는 방법이다.
예시를 들어 쉽게 알아보자. L의 경우는 실제 데이터의 결과 값을 나타낸다. S의 경우에는 컴퓨터가 예측을 하는 값이 된다. 만약 실제 결과 값이 B라고 생각해보자. 조금 더 쉽게 알기 위해서 A와 B만 결과 값이 있는 2개의 행을 가진다고 생각해보자. 그러면 L은 B일 때가 1인 값을 가지게 되는 행렬로 나타난다. 이에 대해 컴퓨터의 예측 값으로 Y가 맞았을 때와 틀렸을 때를 구분하여 알아보면 쉽다. 그래프를 통해서 log의 함수는 다음과 같이 나타나게 된다. 여기서 Y 예측 값에 의한 log를 취한 예측 데이터 행렬과 실제 결과 값을 곱하여 cost function이 크게 되면 예측이 틀린 것을 나타내고 크기가 작으면 예측이 맞는 것을 나타내게 된다.
하나의 데이터에 대한 Softmax의 기법과 Logistic 기법의 cost를 구하는 방법을 비교하게 되면 다음과 같은데 실제로는 다음의 방식 두 개가 같은 것을 의미하게 된다. Logistic의 경우는 binary한 경우만을 생각하여 y가 0과 1일 때를 구분 지어주는 y와 1-y를 사용하였는데 이를 행렬의 형태로 바꾸게 되면 cross entropy와 같은 형태로 나타낼 수 있게 된다. 따라서 Logistic cost는 cross entropy의 한 형태라고 할 수 있게 된다.
이제 이러한 cost의 형태를 모든 데이터에 대해 적용을 시키게 되면 학습된 알고리즘을 만들 수 있게 된다.
이제 Gradient descent algorithm을 이용하여 cost function의 최소화를 시키는 값을 찾아낼 수 있게 되어 학습이 마무리가 된다.